DFA [Automata Lecture 2]

Lecture 1에서 보이던 이 사진

 

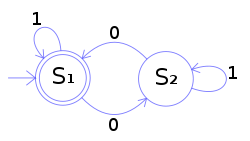
Lecture 1의 Preview에서 소개한게 DFA였다. 사실 나는 아직 강의를 4분 밖에 안들었기 때문에 DFA의 아주아주 기본적인 내용밖에 모른다. 그래서 Preview에서 이 내용을 소개한 것. 이제 강의를 들어나가면서 결정적 유한 오토마타에 대한 자세한 내용을 알아가보겠다.

🌈 Deterministic Finite Automata (DFA)

결정적 유한 오토마타

String으로 Input이 주어지면 Finite State Control을 통해 Accept와 Reject를 결정한다. 예를 들어, Lecture 1 Preview에서는 0이 짝수개인 String에서만 Accept이라고 결정했다. 그렇다면 중요한 것은 Finite State Control!! Accept와 Reject를 결정하는 이 부분에 대해 자세하게 알아보자.

Transition Graph

DFA의 예

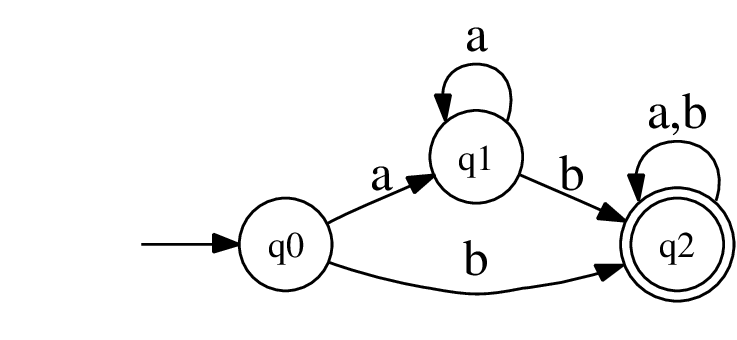
Finite State Control인 Transition Graph는 문자가 적힌 화살표와, 원으로 이뤄져 있다. 화살표를 transition, 원을 state라고 부른다. 이 중, 출발 없이 도착만 있는 화살표는 $q_0$을 가리키는 데, $q_0$는 state 중 시작을 담당한다고 하여 initial 혹은 state state라고 불린다. 원이 겹쳐져서 있는 $q_2$는 이 그래프의 끝이다. final state라고 불린다. 이 state에서 끝난 문자열은 accept라고 결정된다. (이것 이외에 들어오는 모든 state를 reject로 만드는 trap state가 있다.)

process

그렇다면 어떤 과정을 통해 accept와 reject를 결정할까. 먼저, 문자열은 Input된다. 이 문자열을 input file 혹은 tape라고 부른다. 이 상황에서 read head는 tape의 가장 왼쪽 symbol을 가리킨다. Transition Graph에서의 현재 상태는 initial에 있다.

 

aba라는 input file이 들어왔다고 해보자.

1

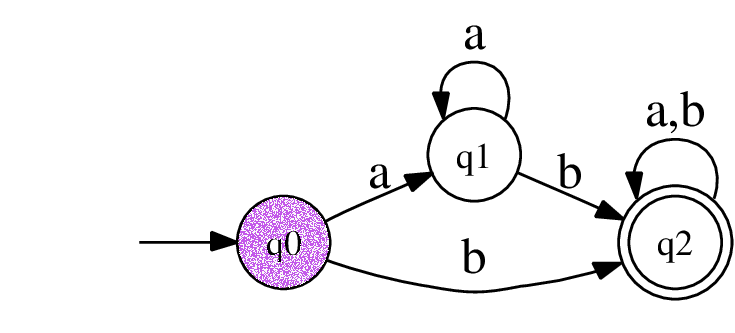
처음에는 read head가 a를 가리킨다. graph에서는 초기의 state에 있다.

 

2

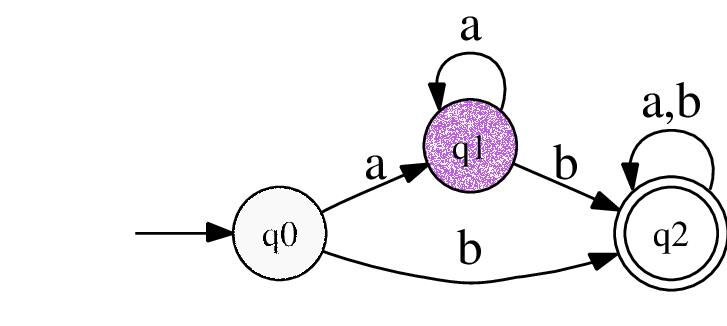
read head가 b를 가리킨다. a를 넘어가면서 Finite State Control에는 a가 입력되었고 a transition을 따라 state는 $q_1$으로 이동했다.

 

3

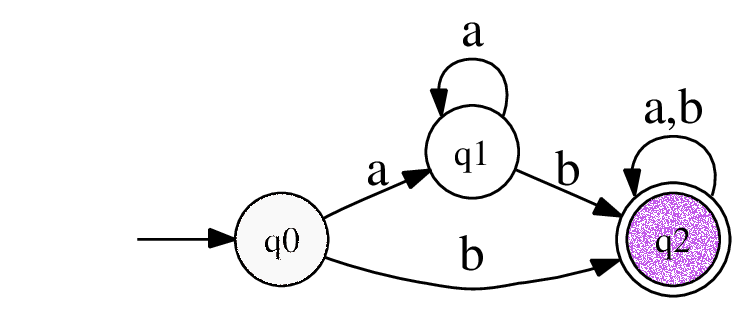
read head가 a를 가리킨다. b를 넘어가면서 Finite State Control에는 b가 입력되었고 b transition을 따라 state는 $q_2$으로 이동했다.

 

4

read head가 빈 공간을 가리킨다. a를 넘어가면서 Finite State Control에는 a가 입력되었고 a transition을 따라 state는 가만히 있다.

 

5

아무것도 입력되지 않아 시스템은 끝이 났고, 현재 state가 final state이므로 Accept라고 판단한다.

 

🌕 Expression

M = (Q, $\Sigma$, $\delta$, $q_0$, F )

• Q : states의 집합
• $\Sigma$ : input alphabet
• $\delta$ : transition function     (ex, $\delta$($q_0$,a=$q_1$))
• $\delta^*$ : transition function (단, 두 번째 인자가 alphabet이다.)   (ex, $\delta$($q_0$,aab=$q_2$))
• $q_0$ : initial state
• F : final states의 집합

---

 L(M)은 DFA M로 부터 accept라고 판단되는 Language(input String들의 집합)이다. 즉, 다음 식이 성립된다.

$$L(M) = \{w|w\in\Sigma^*, \delta ^*(q_0,w)\in F \}$$

 

Regular Languages

Language 중에서 L(M)으로 만들 수 있는 Language를 Regular Language라고 한다. 여기서 M은 어떤 DFA든지 가능하다. 즉, Language가 주어졌을 때 이 Language를 L(M)의 결과값으로 하는 DFA를 만들 수 있다면 그 Language는 Regular Language이다. 예를 들어 b가 하나라도 있는 모든 String들의 집합인 Language는 Regular Language이다. 위에서 과정을 살펴본 DFA의 L(M)이 b가 하나라도 있는 모든 String들의 집합이기 때문이다. 그렇다면 모든 Language가 Regular Language이지 않냐라고 할 수 있는데, 반례가 있다. 다음 Language는 Regular Language를 만드는 DFA를 만들 수 없다. $$L=\{a^nb^n|n \geq 0\}$$