Introduce [Automata Lecture 1]

 

😵 Info 오토마타

개념을 익힌다기보단 이런게 있나보다하는 마음으로 가볍게 넘어가자. Info 부분은 사실 검증이 안되어 있다.

오토마타를 공부하기 전에 오토마타가 뭔지랑 왜 오토마타를 공부해야하는지 알아보자. 구글에 오토마타를 검색해보니 오토마타 이론이 계산 능력이 있는 추상 기계와 그 기계를 이용해서 풀 수 있는 문제들을 연구한다고 한다. 그러니까, 특정한 규칙을 정의하고 그 규칙 내에서 문제를 해결하는 한붓그리기, 스토커 등의 문제들과 비슷한거라 할 수 있지 않을까.

결정적 유한 오토마타의 예

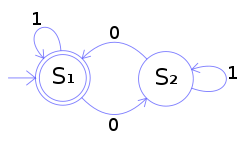
 Preview라는 명목으로 개념을 살짝 던져보겠다. 원과 화살표 그리고 0과 1이라는 문자로 이뤄진 위 사진에서 다음과 같은 규칙을 정해보자. $S_1$에서 시작해 화살표를 통해 문자를 하나씩 더해갈 수 있고 완성된 문자열이 다시 $S_1$에 도착했을 때 참이라는 규칙. 예를 들어 $S_2$로 이동했다가 바로 $S_1$으로 이동했을 때 완성되는 00같은 문자열 말이다. 이러한 규칙 속에서 살펴볼 때, 참이되는 문자열은 늘 0이 짝수개이다. 반대로, 0이 홀수개라면 늘 이 규칙에선 $S_2$에 머물게 된다. 이는 거짓을 의미한다.

위 사진 기호들의 조합은 일정한 규칙 아래, "0이 짝수 개이다"라는 문자열의 참과 거짓을 검증하는 장치를 만들어냈다. 마찬가지로 "1이 홀수개인 문자열"에 대응되는 기호들의 조합도 있을 것이다. 어떤 기호일까. 그러한 기호를 생각해내는 문제. 이 문제의 해답을 고민하게 두며 오토마타에 대한 Preview를 마친다.

---

🕐 Basic Word Concept

Automata의 개념들을 알기 위해, Automata에서 쓰이는 말들의 의미를 알아두자

Basic of Basic

Word	Concept	Example
Symbol	문자 하나 하나 (주로 a,b,c,d 이용)	a
Alphabets ($\Sigma$)	Symbol들의 집합	$\Sigma$ = {a, b}
Strings	Symbol들의 조합 (주로 u,v,w 이용)	u = aabababa
Empty String	길이가 0인 String	$\lambda$
Sigma Star ($\Sigma^*$)	주어진 alphabet으로 만들 수 있는 모든 strings	$\Sigma^*$ = {$\lambda$, a, b , aa, abab ... }
Sigma Plus ($\Sigma^+$)	Empty String을 제외한 Sigma Star	$\Sigma^+$ = {a, b , aa, abab ... }
Languages	Sigma Star의 부분 집합	{$\lambda$, a}

 

Operations + else

Word	Concept	Example
Concatenation	두 String을 연결	wv = aabbbabab
Reverse	거꾸로	$w^R$ = bbaa
Length	길이	$|w|$ = 4
Substring	부분 String	앞에서부터 Substring이면 Prefixes 뒤에서부터 Substring이면 Suffixes
squared	문자열을 여러번 Concatenation	$w^2$ = aabbaabb

---

🕐 Grammar 

Language를 정의하는 또 다른 방법

G = (V, T, S, P)

• V = variables
• T = symbols
• S = Start variable
• P = Productions

Example

Grammar :  S → aSb, S → $\lambda$

S ⇒ aSb ⇒ aaSbb ⇒ aaaSbbb ⇒ aaabbb

 

문법에 의해 만들어지는 친구들을 Sentential Forms이라고 부르며 이 과정들은 ⇒ 기호를 통해 표기한다. 결과적으로 만들어지는 문자열을 String(sentence)라고 부른다. 이 과정들은 Productions을 통해 이뤄지고 Productions을 표기할 때는 →기호를 사용한다. ⇒기호를 여러번 적을 때 번거롭다면 $\overset{ \ast }{\Longrightarrow}$를 사용해 여러 과정들을 생략할 수 있다. ($\overset{ \ast }{\Longrightarrow}$ 붙인 기호는 자기 자신을 가리켜도 된다.)